Clumsy Equations

Less Clumsy Equation

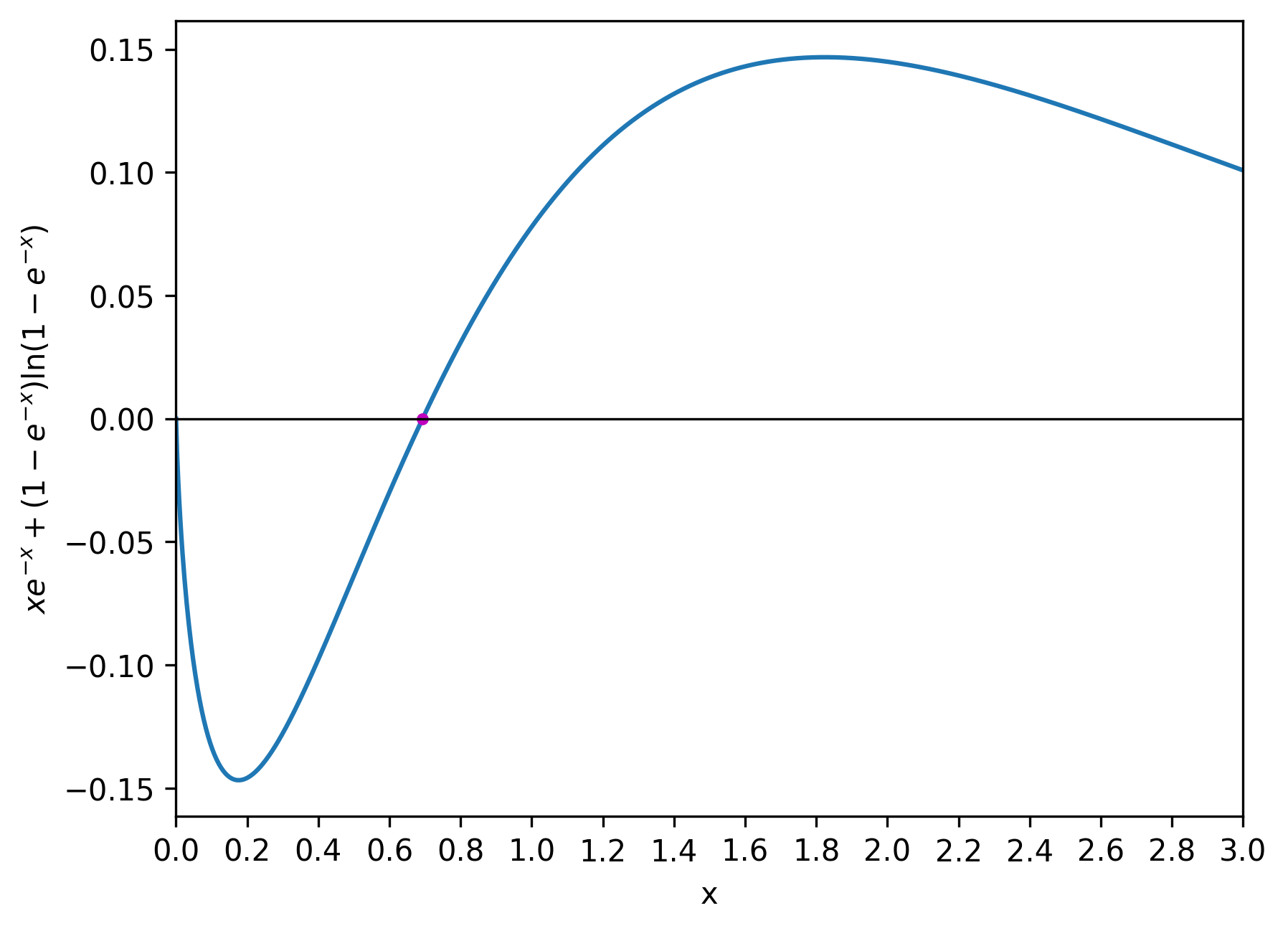
At work today, while calculating optimal parameters for a data structure, I arrived at this equation: \[ x e^{-x} + (1 - e^{-x}) \ln (1 - e^{-x}) = 0. \] This equation is a little clumsy to deal with. Let us make this neat by substituting \( e^{-x} \) with \( t. \) Now we get \[ -t \ln t + (1 - t) \ln (1 - t) = 0. \] If we rearrange this equation as \[ t \ln t = (1 - t) \ln (1 - t), \] it is easy to see that one of the solutions is \( t = 1 - t, \) thus \( t = \frac{1}{2}. \) Are there more solutions to this equation? The answer turns out to be: no.

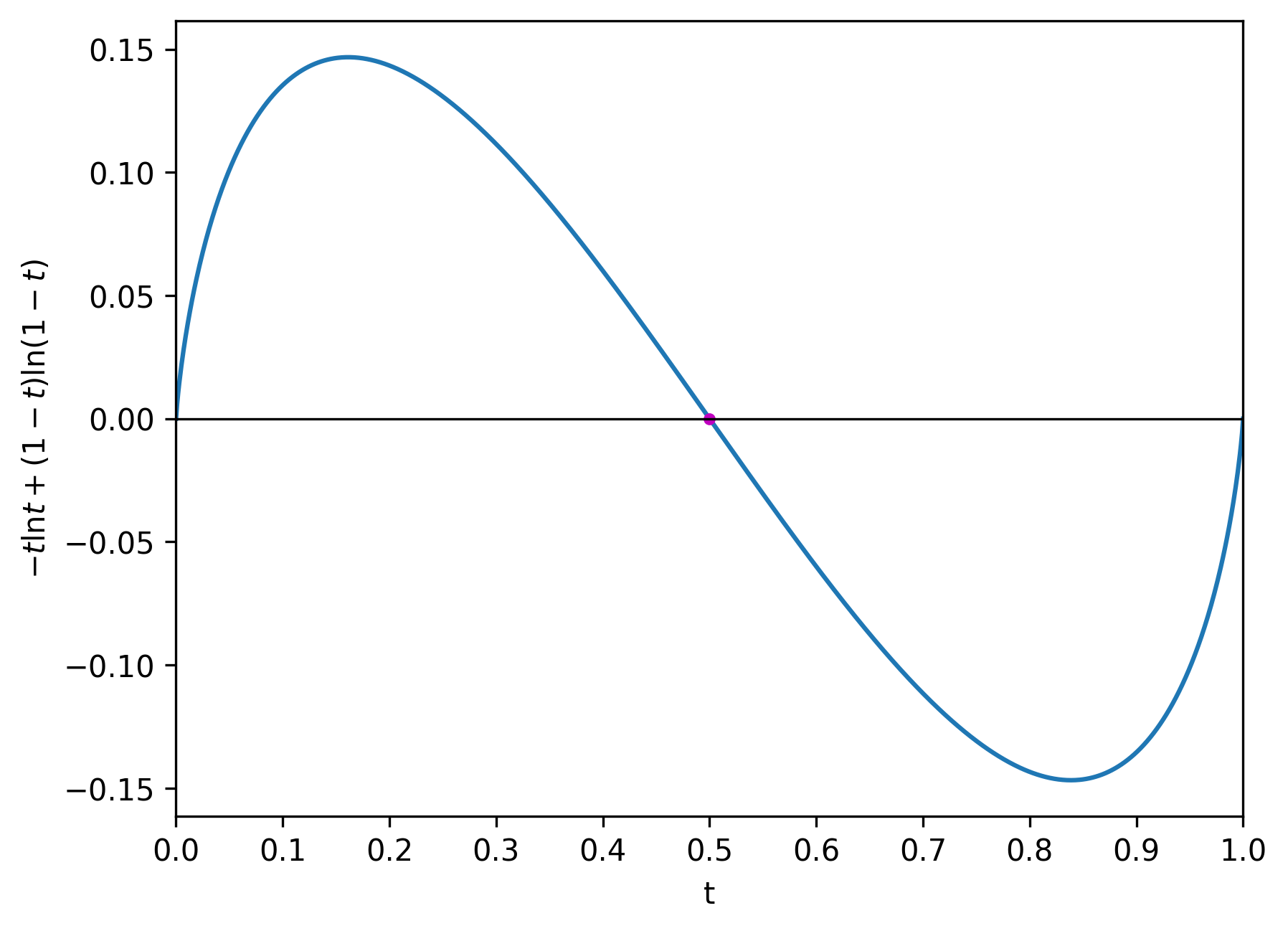
In this problem, \( x \) is a real number and so is \( t. \) In the domain of real numbers, \( \ln t \) is undefined for \( t \le 0. \) As a result, \( \ln (1 - t) \) is undefined for \( t \ge 1. \) Therefore we need to look for values of \( t \) in the open interval \( (0, 1) \) that could be solutions to the equation.

The function \( \ln t \) is a strictly increasing function for \( t > 0. \) This is easy to show from the derivative of \( \ln t. \) The derivative of \( \ln t \) is \( \frac{1}{t} \) which is strictly positive for \( t > 0. \)

Since \( \ln t \) is a strictly increasing function for \( t > 0, \) we can make the following conclusions:

• For \( 0 < t < \frac{1}{2}, \) \( t < (1 - t) \implies t \ln t < (1 - t) \ln (1 - t). \)
• For \( \frac{1}{2} < t < 1, \) \( t > (1 - t) \implies t \ln t > (1 - t) \ln (1 - t). \)

This proves that there are no values of \( t \) in the open intervals \( \left( 0, \frac{1}{2} \right) \) and \( \left( \frac{1}{2}, 1 \right) \) that could be solutions to the equation. Therefore \( t = \frac{1}{2} \) is the only solution to the equation.

Since \( t = e^{-x}, \) we now arrive at the solution to the original equation expressed in terms of \( x \) as follows: \begin{align*} t = \frac{1}{2} & \iff e^{-x} = \frac{1}{2} \\ & \iff -x = \ln \frac{1}{2} \\ & \iff x = \ln 2 \approx 0.6931. \end{align*}

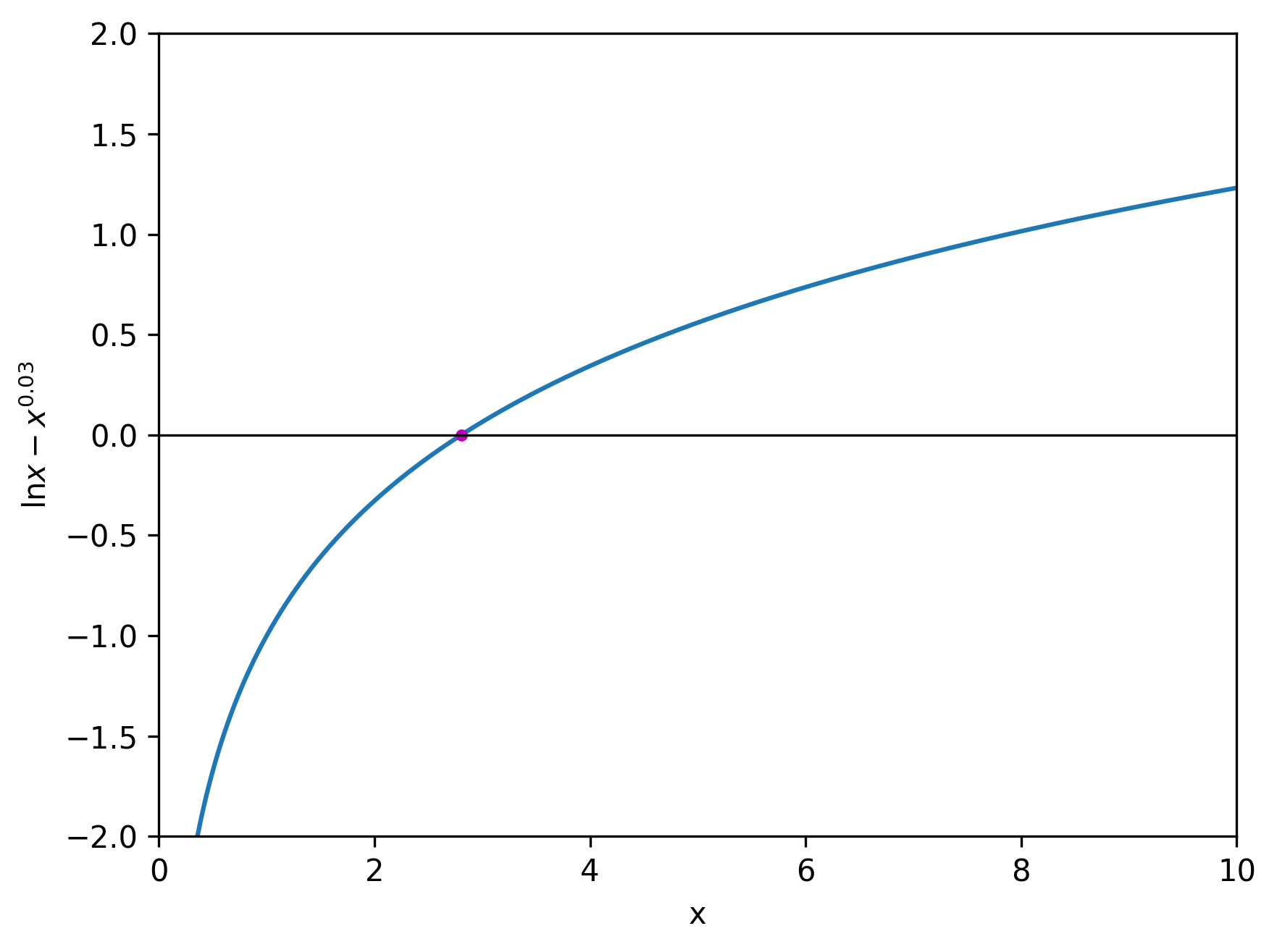
More Clumsy Equation

Here is another equation that I had to solve a couple of years ago: \[ \ln x - x^{0.03} = 0. \] There is no simple way to solve this equation. I had to resort to using the Lambert W function to solve this. To use this function, we first need to bring our equation to the form \( f(x) e^{f(x)} = Y \) where \( f(x) \) is a function of \( x \) and \( Y \) is an expression that does not contain \( x. \) The solution of \( f(x) e^{f(x)} = Y \) is \( f(x) = W(Y). \) To summarise: \[ f(x) e^{f(x)} = Y \iff f(x) = W(Y). \] Applying this technique to our equation, we get \begin{align*} \ln x - x^{0.03} = 0 & \iff \ln x = x^{0.03} \\ & \iff \ln x = e^{0.03 \ln x} \\ & \iff (\ln x)(e^{-0.03 \ln x}) = 1 \\ & \iff (-0.03 \ln x)(e^{-0.03 \ln x}) = -0.03. \\ \end{align*} We have brought the equation to the desired \( f(x) e^{f(x)} = Y \) form where \( f(x) = -0.03 \ln x \) and \( Y = -0.03. \) Therefore the solution to this equation is \[ -0.03 \ln x = W(-0.03). \] Simplifying this further, we get \[ x = e^{\frac{W(-0.03)}{-0.03}}. \] The Maclaurin series of \( W(x) \) is given by \[ W(x) = \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!} x^n = x - x^2 + \frac{3}{2} x^3 - \frac{8}{3} x^4 + \frac{125}{24} x^5 - \dots \] Using the Maclaurin series of \( W(x), \) we get \[ W(-0.03) \approx -0.0309428. \] Therefore \[ x = e^{\frac{W(-0.03)}{-0.03}} \approx e^{\frac{-0.0309428}{-0.03}} \approx 2.80506. \]