When Worse Is Better
Decision Problem
Let me begin this post with a puzzle.
Alex and Bob work as financial advisers for the same company. They receive equal salaries from the company. They behave well at office. Both work on similar assignments. Each assignment required a yes-no decision. The company uses the decisions made by them to make profits.
After the recession hit the company very badly, they have to fire one of them. Both Alex and Bob have worked on almost the same number of assignments in the last ten years. Alex has been consistently taking about 80% decisions correctly every year. Bob, on the other hand, has been taking only about 5% correct decisions every year.
The company decides to keep Bob and fire Alex. Why?
This is a good time to pause and think about the puzzle. There are spoilers ahead.
Capacity of Binary Symmetric Channel
We will come back to the puzzle. Let us discuss the capacity of a binary symmetric channel for a while.
The capacity of a binary symmetric channel with probability of error \( p \) is \[ 1 + p \log_2 p + (1 - p) \log_2 (1 - p). \] The probability of error \( p \) is the probability that the channel will corrupt a bit from 1 to 0 and vice versa. The channel capacity is a measure of the amount of information that is possible to transmit over a channel.
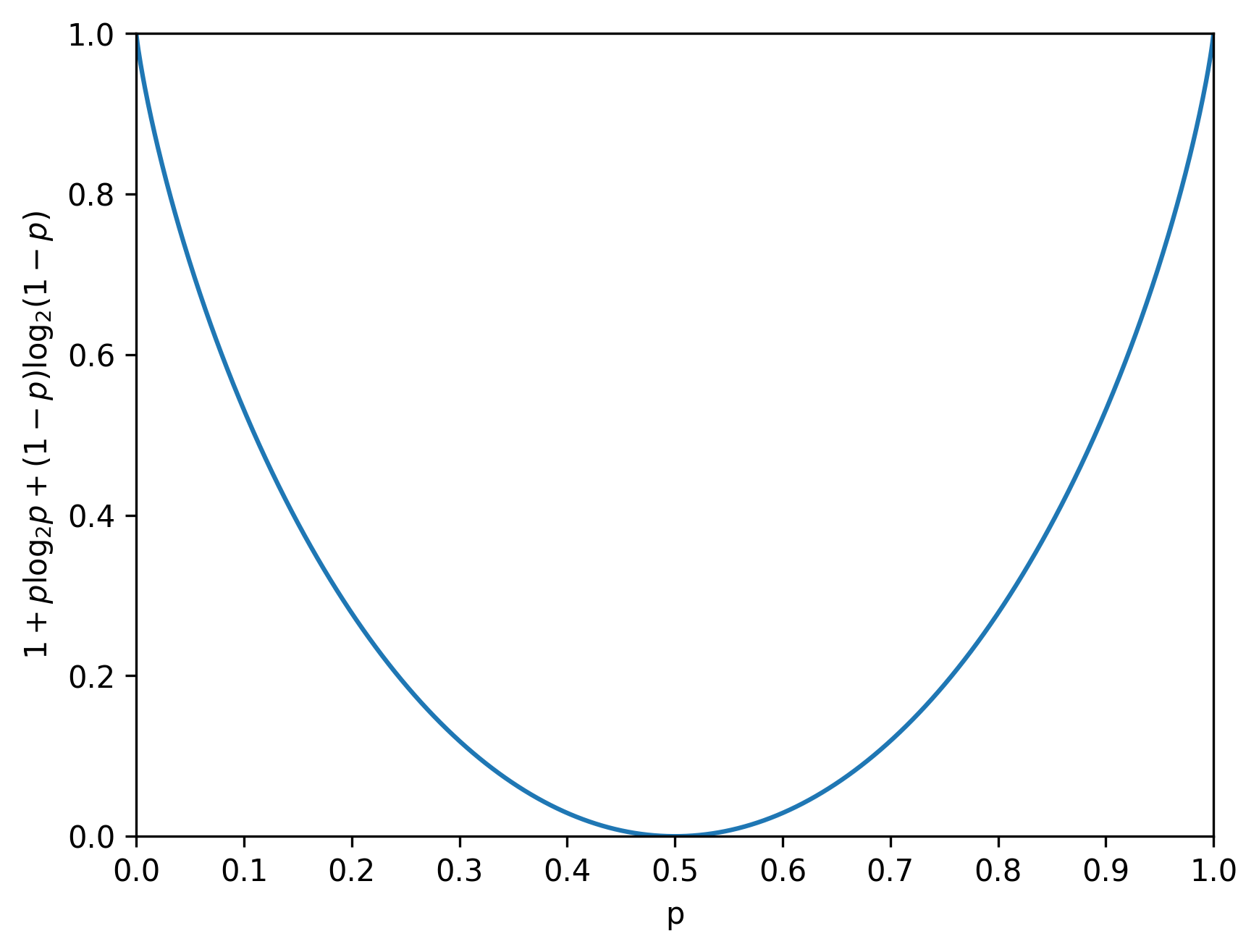
If \( p = 0, \) the channel capacity is maximum. Roughly speaking, if the channel almost never corrupts a bit being transmitted, then the entire channel capacity can be used for data transmission.
If \( p = \frac{1}{2}, \) the channel capacity is zero. In this case, each bit received on the receiver's end is completely random. The channel is equally likely to send 0 or 1 irrespective of the original bit sent by the transmitter.
What might be surprising is that as the probability of error increases from \( \frac{1}{2} \) to \( 1, \) the channel capacity increases. When \( p = 1, \) the channel capacity is maximum again. It is easy to understand this intuitively. At \( p = 1, \) the channel almost surely corrupts every bit. Therefore the receiver can almost surely correct the error by inverting each bit in the received message.
Solution to Decision Problem
Let us get back to the puzzle now.
The company decides to keep Bob because he is more useful to the company. He helps the company to take 95% correct decisions. The company simply does the opposite of what Bob recommends and makes huge profits. Alex on the other hand helps them take only 80% decisions correctly, so he has to go. It is unfair but it is more profitable.